Perform spatial error estimation and variable importance assessment

sperrorest is a flexible interface for multiple types of parallelized spatial and non-spatial cross-validation and bootstrap error estimation and parallelized permutation-based assessment of spatial variable importance.

sperrorest(
  formula,
  data,
  coords = c("x", "y"),
  model_fun,
  model_args = list(),
  pred_fun = NULL,
  pred_args = list(),
  smp_fun = partition_cv,
  smp_args = list(),
  train_fun = NULL,
  train_param = NULL,
  test_fun = NULL,
  test_param = NULL,
  err_fun = err_default,
  imp_variables = NULL,
  imp_permutations = 1000,
  imp_sample_from = c("test", "train", "all"),
  importance = !is.null(imp_variables),
  distance = FALSE,
  do_gc = 1,
  progress = "all",
  benchmark = FALSE,
  mode_rep = c("future", "sequential", "loop"),
  mode_fold = c("sequential", "future", "loop"),
  verbose = 0
)

Arguments

formula: A formula specifying the variables used by the model. Only simple formulas without interactions or nonlinear terms should be used, e.g. y~x1+x2+x3 but not y~x1*x2+log(x3). Formulas involving interaction and nonlinear terms may possibly work for error estimation but not for variable importance assessment, but should be used with caution. The formula y~... is not supported, but y~1 (i.e. no predictors) is.
data: a data.frame with predictor and response variables. Training and test samples will be drawn from this data set by train_fun and test_fun, respectively.
coords: vector of length 2 defining the variables in data that contain the x and y coordinates of sample locations.
model_fun: Function that fits a predictive model, such as glm or rpart. The function must accept at least two arguments, the first one being a formula and the second a data.frame with the learning sample.
model_args: Arguments to be passed to model_fun (in addition to the formula and data argument, which are provided by sperrorest)
pred_fun: Prediction function for a fitted model object created by model. Must accept at least two arguments: the fitted object and a data.frame newdata with data on which to predict the outcome.
pred_args: (optional) Arguments to pred_fun (in addition to the fitted model object and the newdata argument, which are provided by sperrorest).
smp_fun: A function for sampling training and test sets from data. E.g. partition_kmeans for spatial cross-validation using spatial k-means clustering.
smp_args: (optional) Arguments to be passed to smp_fun.
train_fun: (optional) A function for resampling or subsampling the training sample in order to achieve, e.g., uniform sample sizes on all training sets, or maintaining a certain ratio of positives and negatives in training sets. E.g. resample_uniform or resample_strat_uniform.
train_param: (optional) Arguments to be passed to resample_fun.
test_fun: (optional) Like train_fun but for the test set.
test_param: (optional) Arguments to be passed to test_fun.
err_fun: A function that calculates selected error measures from the known responses in data and the model predictions delivered by pred_fun. E.g. err_default (the default).
imp_variables: (optional; used if importance = TRUE). Variables for which permutation-based variable importance assessment is performed. If importance = TRUE and imp_variables == NULL, all variables in formula will be used.
imp_permutations: (optional; used if importance = TRUE). Number of permutations used for variable importance assessment.
imp_sample_from: (default: "test"): specified if the permuted feature values should be taken from the test set, the training set (a rather unlikely choice), or the entire sample ("all"). The latter is useful in leave-one-out resampling situations where the test set is simply too small to perform any kind of resampling. In any case importances are always estimates on the test set. (Note that resampling with replacement is used if the test set is larger than the set from which the permuted values are to be taken.)
importance: logical (default: FALSE): perform permutation-based variable importance assessment?
distance: logical (default: FALSE): if TRUE, calculate mean nearest-neighbour distances from test samples to training samples using add.distance.represampling.
do_gc: numeric (default: 1): defines frequency of memory garbage collection by calling gc; if < 1, no garbage collection; if >= 1, run a gc after each repetition; if >= 2, after each fold.
progress: character (default: all): Whether to show progress information (if possible). Default shows repetition, fold and (if enabled) variable importance progress. Set to "rep" for repetition information only or FALSE for no progress information.
benchmark: (optional) logical (default: FALSE): if TRUE, perform benchmarking and return sperrorestbenchmark object.
mode_rep, mode_fold: character (default: "future" and "sequential", respectively): specifies whether to parallelize the execution at the repetition level, at the fold level, or not at all. Parallel execution uses future.apply::future_lapply() (see details below). It is only possible to parallelize at the repetition level or at the fold level. The "loop" option uses a for loop instead of an lappy function; this option is for debugging purposes.
verbose: Controls the amount of information printed while processing. Defaults to 0 (no output).

Value

A list (object of class sperrorest) with (up to) six components:

error_rep: sperrorestreperror containing predictive performances at the repetition level
error_fold: sperroresterror object containing predictive performances at the fold level
represampling: represampling object
importance: sperrorestimportance object containing permutation-based variable importances at the fold level
benchmark: sperrorestbenchmark object containing information on the system the code is running on, starting and finishing times, number of available CPU cores and runtime performance
package_version: sperrorestpackageversion object containing information about the sperrorest package version

Details

Custom predict functions passed to pred_fun, which consist of multiple child functions, must be defined in one function.

Parallelization

Running in parallel is supported via package future. Have a look at vignette("future-1-overview", package = "future"). In short: Choose a backend and specify the number of workers, then call sperrorest() as usual. Example:

future::plan(future.callr::callr, workers = 2)
sperrorest()

Parallelization at the repetition is recommended when using repeated cross-validation. If the 'granularity' of parallelized function calls is too fine, the overall runtime will be very poor since the overhead for passing arguments and handling environments becomes too large. Use fold-level parallelization only when the processing time of individual folds is very large and the number of repetitions is small or equals 1.

Note that nested calls to future are not possible. Therefore a sequential sperrorest call should be used for hyperparameter tuning in a nested cross-validation.

References

Brenning, A. 2012. Spatial cross-validation and bootstrap for the assessment of prediction rules in remote sensing: the R package 'sperrorest'. 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), 23-27 July 2012, p. 5372-5375. https://ieeexplore.ieee.org/document/6352393

Brenning, A. 2005. Spatial prediction models for landslide hazards: review, comparison and evaluation. Natural Hazards and Earth System Sciences, 5(6), 853-862. doi:10.5194/nhess-5-853-2005

Brenning, A., S. Long & P. Fieguth. 2012. Detecting rock glacier flow structures using Gabor filters and IKONOS imagery. Remote Sensing of Environment, 125, 227-237. doi:10.1016/j.rse.2012.07.005

Russ, G. & A. Brenning. 2010a. Data mining in precision agriculture: Management of spatial information. In 13th International Conference on Information Processing and Management of Uncertainty, IPMU 2010; Dortmund; 28 June - 2 July 2010. Lecture Notes in Computer Science, 6178 LNAI: 350-359.

Russ, G. & A. Brenning. 2010b. Spatial variable importance assessment for yield prediction in Precision Agriculture. In Advances in Intelligent Data Analysis IX, Proceedings, 9th International Symposium, IDA 2010, Tucson, AZ, USA, 19-21 May 2010. Lecture Notes in Computer Science, 6065 LNCS: 184-195.

Examples


## ------------------------------------------------------------
## Classification tree example using non-spatial partitioning
## ------------------------------------------------------------

# Muenchow et al. (2012), see ?ecuador
fo <- slides ~ dem + slope + hcurv + vcurv + log.carea + cslope

library(rpart)
mypred_part <- function(object, newdata) predict(object, newdata)[, 2]
ctrl <- rpart.control(cp = 0.005) # show the effects of overfitting
# show the effects of overfitting
fit <- rpart(fo, data = ecuador, control = ctrl)

### Non-spatial cross-validation:
mypred_part <- function(object, newdata) predict(object, newdata)[, 2]
nsp_res <- sperrorest(
  data = ecuador, formula = fo,
  model_fun = rpart,
  model_args = list(control = ctrl),
  pred_fun = mypred_part,
  progress = TRUE,
  smp_fun = partition_cv,
  smp_args = list(repetition = 1:2, nfold = 3)
)
#> Thu Nov 21 04:24:16 2024 Repetition 1 
#> Thu Nov 21 04:24:16 2024 Repetition - Fold 1 
#> Thu Nov 21 04:24:16 2024 Repetition - Fold 2 
#> Thu Nov 21 04:24:16 2024 Repetition - Fold 3 
#> Thu Nov 21 04:24:16 2024 Repetition 2 
#> Thu Nov 21 04:24:16 2024 Repetition - Fold 1 
#> Thu Nov 21 04:24:16 2024 Repetition - Fold 2 
#> Thu Nov 21 04:24:16 2024 Repetition - Fold 3 
summary(nsp_res$error_rep)
#>                           mean           sd       median          IQR
#> train_auroc          0.8413531 0.0002190341    0.8413531 0.0001548805
#> train_error          0.1917443 0.0018831073    0.1917443 0.0013315579
#> train_accuracy       0.8082557 0.0018831073    0.8082557 0.0013315579
#> train_sensitivity    0.8855000 0.0120208153    0.8855000 0.0085000000
#> train_specificity    0.6543825 0.0295801642    0.6543825 0.0209163347
#> train_fpr70          0.2051793 0.0140857925    0.2051793 0.0099601594
#> train_fpr80          0.2559761 0.0042257377    0.2559761 0.0029880478
#> train_fpr90          0.3954183 0.0042257377    0.3954183 0.0029880478
#> train_tpr80          0.6990000 0.0268700577    0.6990000 0.0190000000
#> train_tpr90          0.4380000 0.0212132034    0.4380000 0.0150000000
#> train_tpr95          0.2870000 0.0141421356    0.2870000 0.0100000000
#> train_events      1000.0000000 0.0000000000 1000.0000000 0.0000000000
#> train_count       1502.0000000 0.0000000000 1502.0000000 0.0000000000
#> test_auroc           0.5913347 0.0145196349    0.5913347 0.0102669323
#> test_error           0.3741678 0.0000000000    0.3741678 0.0000000000
#> test_accuracy        0.6258322 0.0000000000    0.6258322 0.0000000000
#> test_sensitivity     0.7420000 0.0169705627    0.7420000 0.0120000000
#> test_specificity     0.3944223 0.0338059019    0.3944223 0.0239043825
#> test_fpr70           0.5517928 0.0084514755    0.5517928 0.0059760956
#> test_fpr80           0.6812749 0.0225372679    0.6812749 0.0159362550
#> test_fpr90           0.8705179 0.0366230604    0.8705179 0.0258964143
#> test_tpr80           0.2720000 0.0678822510    0.2720000 0.0480000000
#> test_tpr90           0.1590000 0.0183847763    0.1590000 0.0130000000
#> test_tpr95           0.0920000 0.0056568542    0.0920000 0.0040000000
#> test_events        500.0000000 0.0000000000  500.0000000 0.0000000000
#> test_count         751.0000000 0.0000000000  751.0000000 0.0000000000
summary(nsp_res$error_fold)
#>                           mean         sd      median         IQR
#> train.auroc         0.83743699 0.02048053   0.8333183 0.033646385
#> train.error         0.19173586 0.01438586   0.1967984 0.014375250
#> train.accuracy      0.80826414 0.01438586   0.8032016 0.014375250
#> train.sensitivity   0.88544232 0.03107595   0.8810630 0.039594807
#> train.specificity   0.65315955 0.07978799   0.6303327 0.123423546
#> train.fpr70         0.21096473 0.03745328   0.2102482 0.039804792
#> train.fpr80         0.26678331 0.04197401   0.2696150 0.055188199
#> train.fpr90         0.41645165 0.05634835   0.4302107 0.027201786
#> train.tpr80         0.67328390 0.09501731   0.7081574 0.136802093
#> train.tpr90         0.42606490 0.02625749   0.4288201 0.038100185
#> train.tpr95         0.24519417 0.10272755   0.2306974 0.135858369
#> train.events      333.33333333 6.47044563 334.0000000 5.750000000
#> train.count       500.66666667 0.51639778 501.0000000 0.750000000
#> test.auroc          0.59363657 0.03339583   0.5821419 0.002435316
#> test.error          0.37417530 0.02708388   0.3712590 0.010470120
#> test.accuracy       0.62582470 0.02708388   0.6287410 0.010470120
#> test.sensitivity    0.74203609 0.03728947   0.7396495 0.067245950
#> test.specificity    0.39550360 0.06362015   0.4024297 0.088476560
#> test.fpr70          0.56470600 0.04071028   0.5440798 0.046597213
#> test.fpr80          0.72560279 0.05383697   0.7249146 0.046820219
#> test.fpr90          0.85173443 0.03938630   0.8563455 0.020751291
#> test.tpr80          0.23524330 0.11922537   0.2271224 0.108842594
#> test.tpr90          0.12384858 0.07164059   0.1309382 0.038435952
#> test.tpr95          0.06825989 0.07977265   0.0511169 0.059644324
#> test.events       166.66666667 6.47044563 166.0000000 5.750000000
#> test.count        250.33333333 0.51639778 250.0000000 0.750000000
#> distance           -1.00000000 0.00000000  -1.0000000 0.000000000
summary(nsp_res$represampling)
#> $`1`
#>   n.train n.test
#> 1     500    251
#> 2     501    250
#> 3     501    250
#> 
#> $`2`
#>   n.train n.test
#> 1     501    250
#> 2     501    250
#> 3     500    251
#> 
# plot(nsp_res$represampling, ecuador)

### Spatial cross-validation:
sp_res <- sperrorest(
  data = ecuador, formula = fo,
  model_fun = rpart,
  model_args = list(control = ctrl),
  pred_fun = mypred_part,
  progress = TRUE,
  smp_fun = partition_kmeans,
  smp_args = list(repetition = 1:2, nfold = 3)
)
#> Thu Nov 21 04:24:16 2024 Repetition 1 
#> Thu Nov 21 04:24:16 2024 Repetition - Fold 1 
#> Thu Nov 21 04:24:16 2024 Repetition - Fold 2 
#> Thu Nov 21 04:24:16 2024 Repetition - Fold 3 
#> Thu Nov 21 04:24:16 2024 Repetition 2 
#> Thu Nov 21 04:24:16 2024 Repetition - Fold 1 
#> Thu Nov 21 04:24:16 2024 Repetition - Fold 2 
#> Thu Nov 21 04:24:16 2024 Repetition - Fold 3 
summary(sp_res$error_rep)
#>                           mean          sd       median         IQR
#> train_auroc          0.8472530 0.017474834    0.8472530 0.012356574
#> train_error          0.1820905 0.002353884    0.1820905 0.001664447
#> train_accuracy       0.8179095 0.002353884    0.8179095 0.001664447
#> train_sensitivity    0.8905000 0.009192388    0.8905000 0.006500000
#> train_specificity    0.6733068 0.011268634    0.6733068 0.007968127
#> train_fpr70          0.1842629 0.029580164    0.1842629 0.020916335
#> train_fpr80          0.2370518 0.011268634    0.2370518 0.007968127
#> train_fpr90          0.3555777 0.012677213    0.3555777 0.008964143
#> train_tpr80          0.7360000 0.053740115    0.7360000 0.038000000
#> train_tpr90          0.4845000 0.067175144    0.4845000 0.047500000
#> train_tpr95          0.2660000 0.024041631    0.2660000 0.017000000
#> train_events      1000.0000000 0.000000000 1000.0000000 0.000000000
#> train_count       1502.0000000 0.000000000 1502.0000000 0.000000000
#> test_auroc           0.5032968 0.024889595    0.5032968 0.017599602
#> test_error           0.4727031 0.028246609    0.4727031 0.019973369
#> test_accuracy        0.5272969 0.028246609    0.5272969 0.019973369
#> test_sensitivity     0.5470000 0.032526912    0.5470000 0.023000000
#> test_specificity     0.4880478 0.019720109    0.4880478 0.013944223
#> test_fpr70           0.7529880 0.061977487    0.7529880 0.043824701
#> test_fpr80           0.8884462 0.056343170    0.8884462 0.039840637
#> test_fpr90           0.9282869 0.000000000    0.9282869 0.000000000
#> test_tpr80           0.1610000 0.004242641    0.1610000 0.003000000
#> test_tpr90           0.0990000 0.007071068    0.0990000 0.005000000
#> test_tpr95           0.0650000 0.018384776    0.0650000 0.013000000
#> test_events        500.0000000 0.000000000  500.0000000 0.000000000
#> test_count         751.0000000 0.000000000  751.0000000 0.000000000
summary(sp_res$error_fold)
#>                           mean          sd       median          IQR
#> train.auroc         0.84515941  0.01905839   0.84534979  0.028026750
#> train.error         0.18240710  0.01060702   0.18304622  0.009904172
#> train.accuracy      0.81759290  0.01060702   0.81695378  0.009904172
#> train.sensitivity   0.88941674  0.01990945   0.88819737  0.018551212
#> train.specificity   0.67338381  0.03405612   0.67399773  0.033408639
#> train.fpr70         0.19001989  0.02696925   0.18629168  0.035076259
#> train.fpr80         0.26077121  0.03429704   0.25571965  0.040338724
#> train.fpr90         0.38765695  0.03869441   0.38784530  0.057629711
#> train.tpr80         0.69871754  0.06961726   0.71852900  0.077197624
#> train.tpr90         0.38222915  0.12415524   0.37383597  0.127049184
#> train.tpr95         0.24811503  0.08804794   0.21752928  0.118033864
#> train.events      333.33333333 44.88503834 326.50000000 50.500000000
#> train.count       500.66666667 52.87217290 490.00000000 65.500000000
#> test.auroc          0.52865230  0.04745692   0.53136288  0.078210920
#> test.error          0.46155050  0.07803414   0.43884387  0.080997314
#> test.accuracy       0.53844950  0.07803414   0.56115613  0.080997314
#> test.sensitivity    0.58378570  0.19028544   0.64871054  0.191650843
#> test.specificity    0.47751069  0.16408495   0.45386905  0.161617488
#> test.fpr70          0.74420320  0.12039194   0.75586762  0.182721973
#> test.fpr80          0.84903452  0.12630703   0.87089783  0.074518397
#> test.fpr90          0.96263035  0.03429537   0.95823650  0.044154776
#> test.tpr80          0.15410646  0.07515119   0.15269750  0.066471765
#> test.tpr90          0.10004200  0.06560359   0.12034188  0.094070539
#> test.tpr95          0.04934735  0.07259254   0.01269036  0.075709340
#> test.events       166.66666667 44.88503834 173.50000000 50.500000000
#> test.count        250.33333333 52.87217290 261.00000000 65.500000000
#> distance           -1.00000000  0.00000000  -1.00000000  0.000000000
summary(sp_res$represampling)
#> $`1`
#>   n.train n.test
#> 1     498    253
#> 2     573    178
#> 3     431    320
#> 
#> $`2`
#>   n.train n.test
#> 1     482    269
#> 2     469    282
#> 3     551    200
#> 
# plot(sp_res$represampling, ecuador)

smry <- data.frame(
  nonspat_training = unlist(summary(nsp_res$error_rep,
    level = 1
  )$train_auroc),
  nonspat_test = unlist(summary(nsp_res$error_rep,
    level = 1
  )$test_auroc),
  spatial_training = unlist(summary(sp_res$error_rep,
    level = 1
  )$train_auroc),
  spatial_test = unlist(summary(sp_res$error_rep,
    level = 1
  )$test_auroc)
)
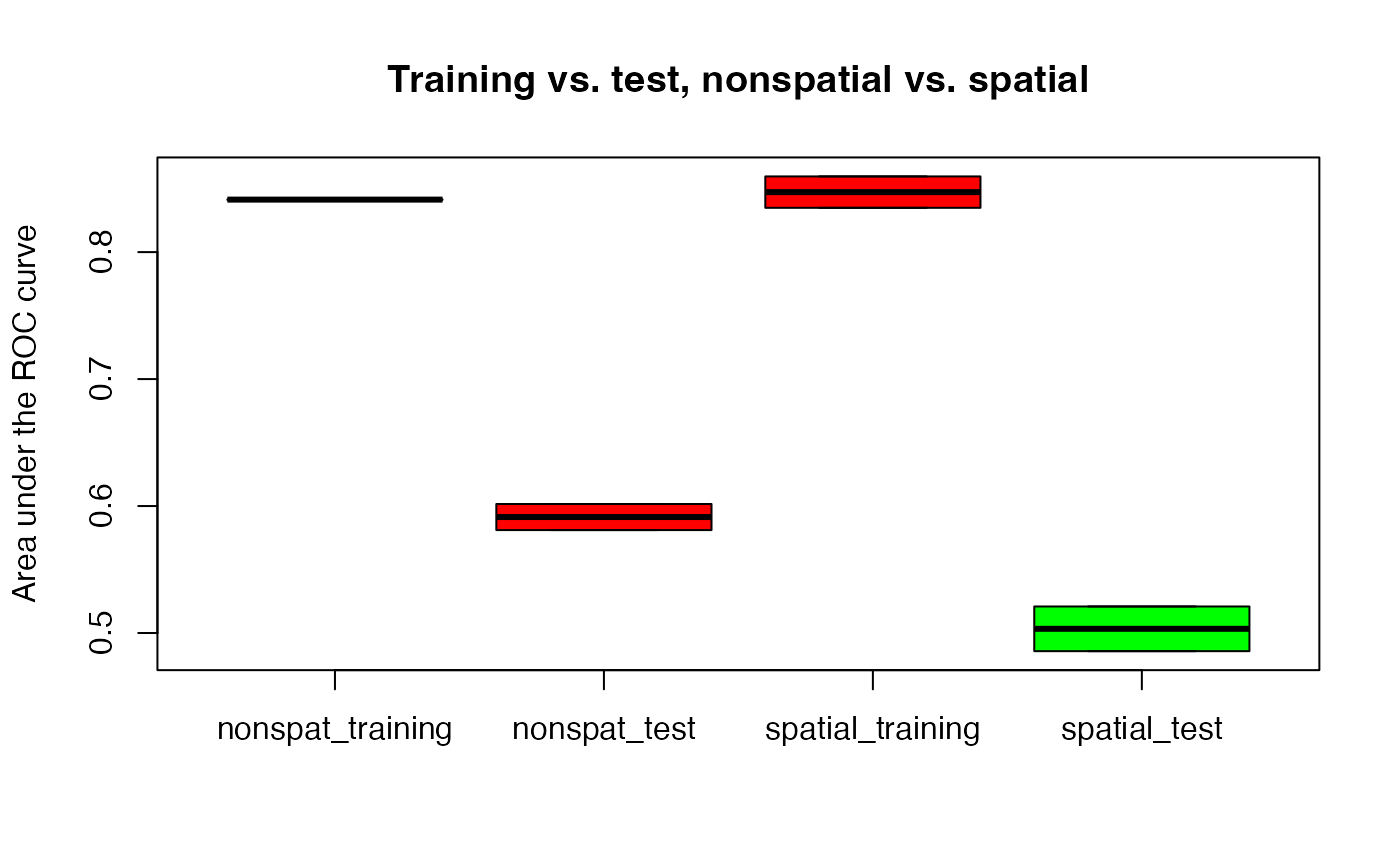
boxplot(smry,
  col = c("red", "red", "red", "green"),
  main = "Training vs. test, nonspatial vs. spatial",
  ylab = "Area under the ROC curve"
)